O algoritmo de Luhn, também chamado de fórmula de Luhn, "módulo 10" ou algoritmo "mod 10", é uma fórmula de soma de verificação simples usada para validar números de identificação. O algoritmo, desenvolvido pelo engenheiro da IBM Hans Peter Luhn, pode ser usado para validar números de cartão de crédito, Identidade Internacional de Equipamento Móvel (IMEI) e outros dados numéricos. Hoje, as empresas costumam usá-lo para aumentar a precisão e a confiabilidade de seus processos de entrada de dados, especialmente ao lidar com informações confidenciais, como dados de pagamento.

Veja aqui o que as empresas precisam saber sobre o algoritmo de Luhn: o que é, por que é tão importante e como usá-lo para aumentar a segurança dos pagamentos dos seus clientes.

Neste artigo:

• Fórmula do algoritmo de Luhn
  
• Por que o algoritmo de Luhn é tão importante?
  
• Que tipo de números o algoritmo de Luhn valida?
  
• Como diferentes setores usam o algoritmo de Luhn?
  
• Limitações do algoritmo de Luhn
  
• Como o Stripe Radar pode ajudar
  

Fórmula do algoritmo de Luhn

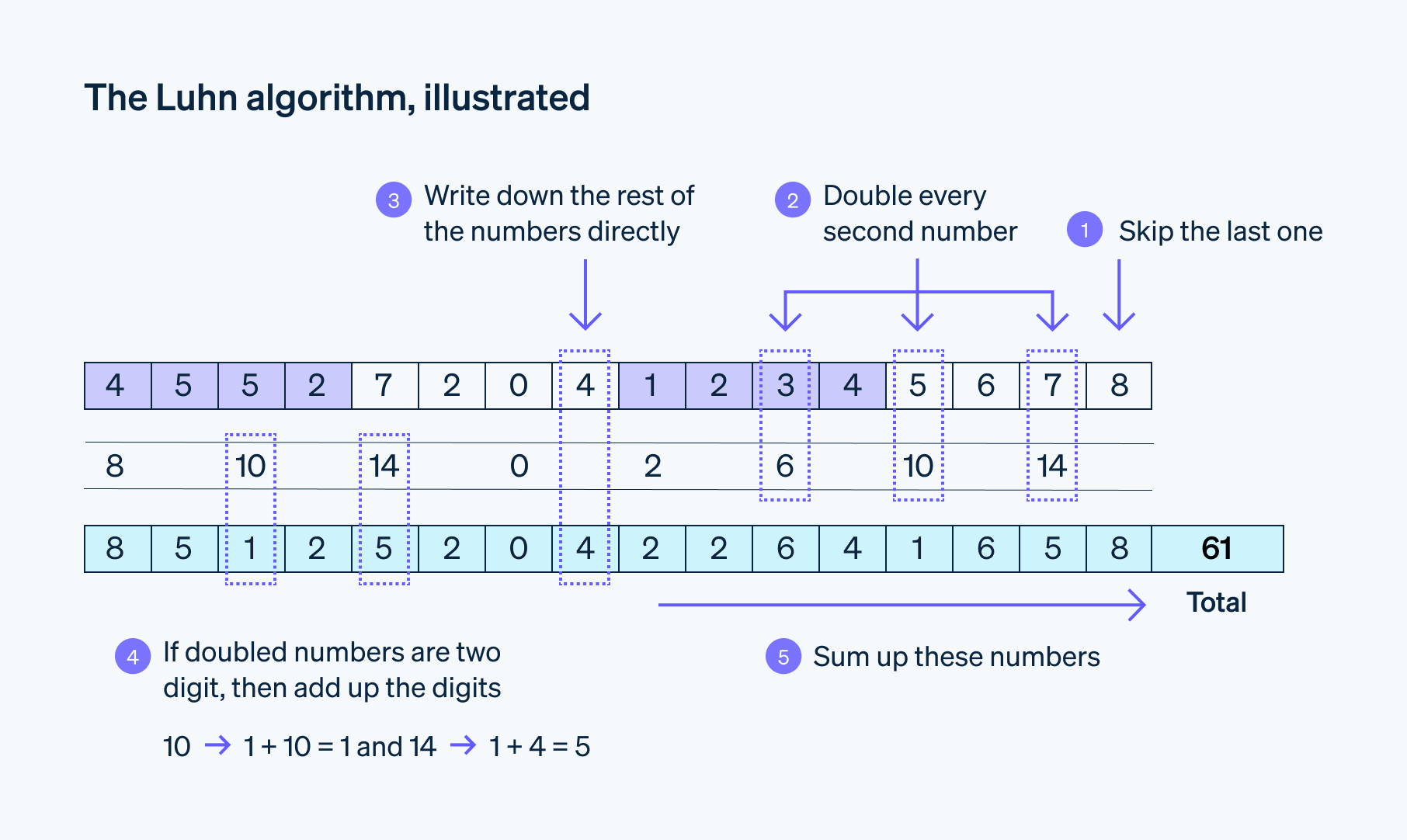
O algoritmo de Luhn não tem uma fórmula no sentido matemático convencional, e sim uma série de etapas.

• Passo 1: multiplique por dois o segundo dígito da direita para a esquerda, pule o próximo, multiplique por dois o seguinte e continue dobrando os dígitos alternados. Se o resultado de qualquer duplicação for maior que 9, some os dígitos do resultado para obter um número de um dígito.
  Exemplo: 6 × 2 = 12; 1 + 2 = 3

• Passo 2: some todos os dígitos que você não dobrou e os novos valores que você obteve com a duplicação.

• Passo 3: veja se a soma é um múltiplo de 10. O número é considerado válido de acordo com o algoritmo de Luhn se o total terminar em 0.

Para ilustrar, vamos verificar o número 79927398713 usando a fórmula do algoritmo de Luhn.

Da direita para a esquerda, pule o primeiro e multiplique por dois o segundo dígito, pule o próximo e multiplique o quarto, e assim por diante.

1 x 2 = 2

8 x 2 = 16 (1 + 6 = 7)

3 × 2 = 6

2 × 2 = 4

9 x 2 = 18 (1 + 8 = 9)

Some todos os dígitos, inclusive os não duplicados:

7 + 9 + 9 + 4 + 7 + 6 + 9 + 7 + 7 + 2 + 3 = 70

O número 79927398713 é válido de acordo com o algoritmo de Luhn porque o resultado é 70, que é um múltiplo de 10.

Essa é a "fórmula" ou procedimento que o algoritmo de Luhn segue para validar ou gerar números.

Por que o algoritmo de Luhn é tão importante?

O algoritmo de Luhn foi um divisor de águas na validação de dados e prevenção de fraudes em diversos setores, especialmente finanças, pagamentos e serviços governamentais.

Aqui estão algumas razões pelas quais isso é tão importante:

• Maior precisão de dados: o algoritmo de Luhn é um método simples para detectar tipos comuns de erros de entrada, como erros de um dígito ou erros de transposição que invertem dois dígitos, o que é especialmente importante em setores como finanças e bancos.

• Facilidade de implementação: o algoritmo é simples de entender e implementar em várias linguagens de programação e não consome muita computação, tornando-o acessível para diversas aplicações.

• Recursos em tempo real: o algoritmo de Luhn pode ser aplicado em tempo real para verificar a exatidão dos dados numéricos à medida que são inseridos, e tornou-se uma verificação importante para sistemas que exigem validação instantânea de dados.

• Prevenção de fraudes: embora não seja infalível contra tentativas de fraude, o algoritmo de Luhn cria a primeira linha de defesa. Ele ajuda a filtrar números inválidos antes do início de uma transação ou operação, o que pode impedir tentativas de fraude e reduzir a incidência de erros que resultem em fraudes ou violações de segurança.

• Custos mais baixos: ao detectar erros no início do processo, o algoritmo ajuda a evitar custos associados ao processamento incorreto de dados, como perdas financeiras, insatisfação do cliente e custos administrativos da correção de erros.

• Influência global: devido à sua eficácia e simplicidade, o algoritmo de Luhn tem sido amplamente adotado em todo o mundo para validação documentos de identificação pelas maiores empresas de cartão de crédito, órgãos públicos e instituições financeiras.

O algoritmo de Luhn tornou-se uma ferramenta eficaz para verificar cartões de crédito e dados confidenciais, detectando erros, evitando fraudes e garantindo transações precisas. A facilidade de implementação e a validação em tempo real fazem dele uma medida de segurança fundamental no processamento de pagamentos e nos sistemas financeiros.

Que tipos de números o algoritmo de Luhn valida?

Em qualquer sistema onde os números são inseridos manualmente, o algoritmo de Luhn pode ser usado para validação em tempo real, detectando e destacando erros imediatamente, melhorando a qualidade dos dados e a eficiência operacional. Ele garante que as sequências numéricas sejam estruturalmente válidas antes do processamento.

Visão geral dos tipos de sequências numéricas que ele costuma verificar:

• Números de cartão de crédito: o uso mais comum do algoritmo de Luhn é para verificação de cartão de crédito. Antes de uma transação com cartão de crédito ser processada, o número do cartão é verificado pelo algoritmo de Luhn, para confirmar se a sequência é válida. Esta etapa ajuda a detectar erros na digitação ou números incompletos. Quase todos os cartões de crédito têm uma verificação de Luhn.

• Documentos de identificação: o algoritmo de Luhn é usado para validar números de identificação, como números de seguridade social, números IMEI para telefones celulares ou documentos nacionais de identificação. Essa validação verifica se os números foram inseridos e processados corretamente.

• Identificadores financeiros: muitos bancos usam o algoritmo de Luhn para verificar números de conta e outros identificadores financeiros, como routing numbers, antes de processar transferências e outras transações.

• Código de barras: alguns formatos de código de barras, como EAN e UPC, incorporam um dígito de verificação, que é calculado pelo algoritmo de Luhn. Os scanners usam o algoritmo para verificar se os códigos de barras são escaneados corretamente para um rastreamento de estoque mais preciso, checkout de varejo e operações logísticas.

Como diferentes setores usam o algoritmo de Luhn?

O algoritmo de Luhn é usado em diversos setores para verificar dados numéricos críticos, evitar erros de digitação e aprimorar a proteção contra fraudes.

Algumas aplicações práticas comuns do algoritmo de Luhn:

• Compras online: quando você faz uma compra online, o sistema de pagamento usa o algoritmo de Luhn para verificar se você inseriu um número de cartão de crédito válido antes de processar a transação. Isso ajuda a reduzir pagamentos recusados por erros de digitação ou números incorretos.

• Sistemas bancários: bancos e empresas de cartão usam o algoritmo de Luhn para validar números de conta e routing numbers, garantindo que os fundos sejam transferidos para as contas corretas. Isso assegura que os fundos sejam transferidos para contas financeiras válidas antes do processamento das transferências eletrônicas de fundos (TEF) ou dos pagamentos ACH.

• Celulares: os números IMEI (International Mobile Equipment Identity) identificam exclusivamente os dispositivos móveis e incluem um dígito de verificação calculado a partir dos outros dígitos usando o algoritmo de Luhn. Isso ajuda a verificar a integridade do número IMEI, auxiliando na prevenção de fraudes e na identificação do dispositivo ao comprar um telefone usado.

• Documentos governamentais: em alguns países, números de identificação como números de seguridade social ou documentos nacionais de identificação incorporam um dígito de verificação calculado pelo algoritmo de Luhn. Isso ajuda os órgãos públicos a verificarem se os números estão corretos durante a entrada e o processamento de dados em documentos fiscais, benefícios sociais e emissão de documentos.

• Concessionárias de serviços públicos: provedores de serviços públicos geralmente usam o algoritmo de Luhn para validar números de conta do cliente. Isso garante que os dados de cobrança e de pagamento seja associadas às contas corretas, reduzindo erros de faturamento e problemas de atendimento ao cliente.

• Sistemas de bilheteria: companhias aéreas, ferrovias e outras empresas de transporte usam o algoritmo Luhn para validar números de referência de reserva ou números de bilhetes, garantindo que os dados sejam inseridos corretamente e reduzindo o risco de fraude de bilhetes.

Limitações do algoritmo de Luhn

Embora o algoritmo de Luhn seja uma ferramenta poderosa para detecção de erros e validação numérica, ele tem certas limitações. Para detecção de fraudes ou validação de dados, o algoritmo de Luhn faz parte de um conjunto mais extenso de ferramentas; depender exclusivamente dele não é aconselhável em sistemas de segurança críticos.

Algumas das principais limitações do algoritmo de Luhn:

• Detecção de erros complexos: o algoritmo é projetado para capturar erros comuns, como entradas incorretas de um dígito ou transposições de dígitos adjacentes (por exemplo, 67 se tornando 76), mas não detecta erros mais complexos, como troca de dígitos não adjacentes (por exemplo, 197 trocado por 971) ou vários dígitos incorretos seguidos.

• Detecção de fraudes: o algoritmo de Luhn pode verificar se uma sequência de números é válida, mas não pode determinar se corresponde a uma conta ou identidade legítima ou proteger contra atividades fraudulentas, onde o fraudador tem uma sequência numérica válida.

• Dados não numéricos: o algoritmo funciona somente com dados numéricos e não pode ser usado para validar dados que incluem letras, símbolos, caracteres especiais ou identificadores alfanuméricos.

• Integridade dos dados: o algoritmo verifica apenas a validade numérica, não a integridade dos dados. Ele não pode detectar se os dados foram alterados intencionalmente ou identificar qual parte dos dados está incorreta.

• Previsibilidade: o algoritmo é um método padrão bem conhecido e qualquer pessoa com conhecimento do algoritmo pode gerar números que passam na verificação de Luhn. Essa previsibilidade pode ser uma desvantagem em situações em que um nível mais alto de segurança é necessário.

• Aplicação limitada para cibersegurança: como a verificação de Luhn não criptografa nem oculta os dados, ela não fornece segurança contra ataques como hacking, phishing ou violações de dados. Outras medidas de segurança, como criptografia, autenticação multifator (MFA) e detecção de fraudes por IA devem ser usadas junto com ele.

Apesar dessas limitações, o algoritmo de Luhn continua sendo uma ferramenta amplamente utilizada para verificações preliminares de sequências numéricas em diversas aplicações, particularmente em serviços financeiros. Em conjunto com processos adicionais de segurança e verificação, pode melhorar a precisão dos dados e evitar erros acidentais em sequências numéricas.

Como o Stripe Radar pode ajudar

O Stripe Radar usa modelos de IA treinados para detectar e prevenir fraudes usando dados da rede Stripe global. Ele atualiza continuamente esses modelos de acordo com as últimas tendências de fraude, protegendo a empresa contra a evolução das fraudes.

A Stripe também oferece o Radar for Fraud Teams, que permite aos usuários adicionar regras personalizadas que abordam cenários de fraude específicos da sua empresa e acessar insights avançados de fraude.

O Radar pode ajudar sua empresa a:

• Prevenir perdas por fraude: a Stripe processa anualmente mais de US$ 1 trilhão em pagamentos. Essa escala exclusiva permite que o Radar detecte e evite fraudes com precisão, economizando dinheiro.
  
• Aumentar a receita: os modelos de IA do Radar são treinados com dados de contestações reais, informações de clientes, dados de navegação e muitos mais. Isso permite que o Radar identifique transações arriscadas e reduza falsos positivos, aumentando sua receita.
  
• Economizar tempo: o Radar é integrado à Stripe e exige zero linhas de código para ser configurado. Você também pode monitorar o desempenho da prevenção de fraudes, criar regras e muito mais em uma única plataforma, aumentando a eficiência.
  

Saiba mais sobre o Stripe Radar ou comece a usar ainda hoje.