L’algorithme de Luhn, également connu sous le nom de formule de Luhn, « modulo 10 » ou « mod 10 », est une formule simple de somme de contrôle utilisée pour valider des numéros d’identification. Développé par Hans Peter Luhn, ingénieur chez IBM, il peut être utilisé pour valider des numéros de cartes de crédit, des numéros d’identité internationale d’équipement mobile (International Mobile Equipment Identity ou IMEI) et d’autres données numériques. Les entreprises y ont souvent recours pour renforcer la précision et la fiabilité de leurs processus de saisie de données, en particulier lorsqu’elles gèrent des informations sensibles, telles que des données de paiement.

Vous découvrirez ci-dessous en quoi consiste l’algorithme de Luhn, pourquoi il est important et comment l’utiliser pour renforcer la sécurité des paiements de vos clients.

Sommaire

• Formule de l’algorithme de Luhn
  
• Intérêt de l’algorithme de Luhn
  
• Types de numéros validés par l’algorithme de Luhn
  
• Utilisation de l’algorithme de Luhn dans différents secteurs
  
• Limites de l’algorithme de Luhn
  
• Comment Stripe Radar peut aider
  

Formule de l’algorithme de Luhn

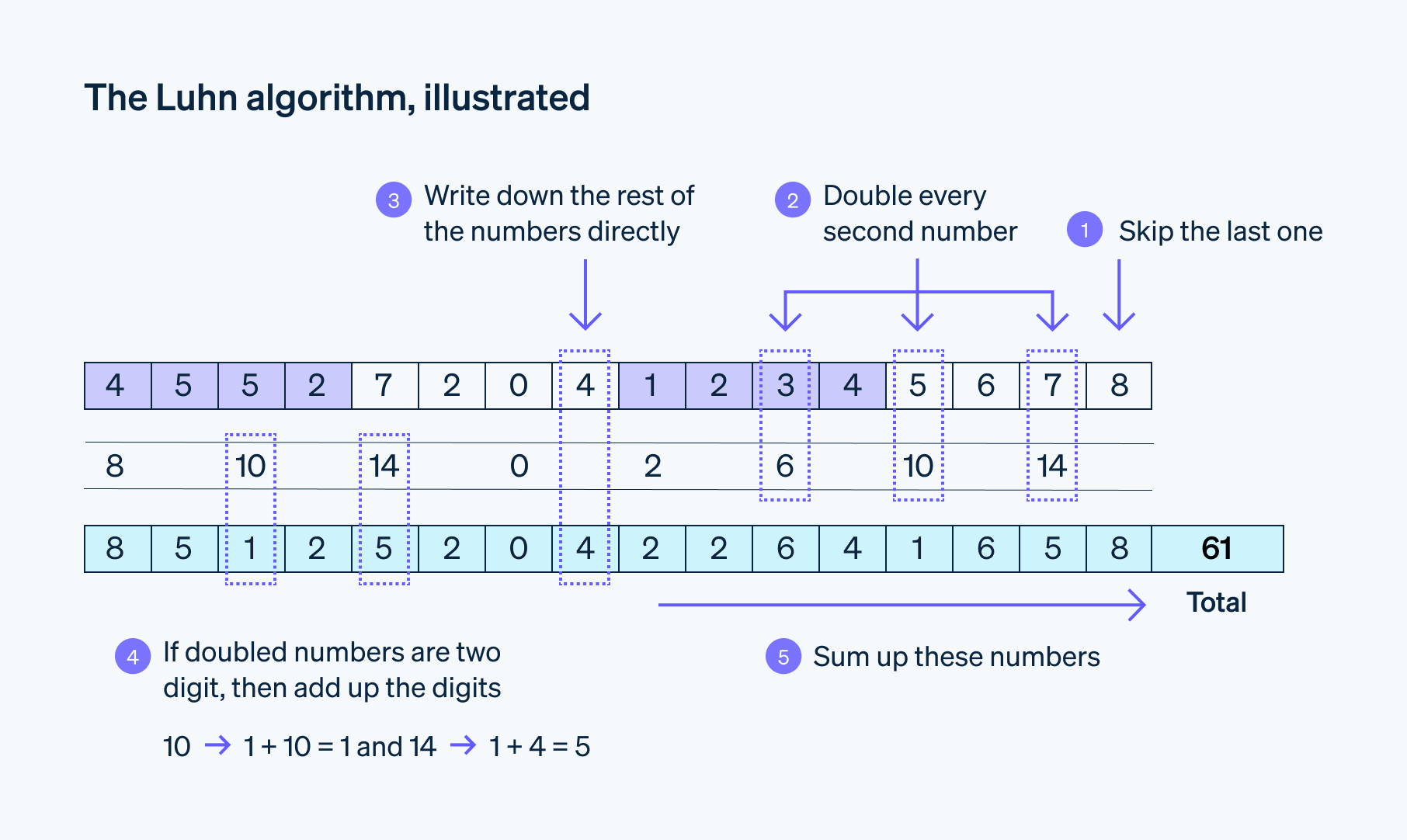
L’algorithme de Luhn n’est pas à proprement parler une formule mathématique conventionnelle. Il est plutôt constitué d’une série d’étapes.

• Étape 1 : en partant de la droite, multipliez par deux la valeur de l’avant-dernier chiffre et répétez l’opération pour un chiffre sur deux. Si le résultat de l’une de ces multiplications est supérieur à 9, additionnez les chiffres de ce résultat pour obtenir un nombre à un seul chiffre.
  Exemple : 6 × 2 = 12 ; 1 + 2 = 3

• Étape 2 : faites la somme de tous les chiffres que vous n’avez pas multipliés par deux et des nouvelles valeurs obtenues par les différentes multiplications par deux.

• Étape 3 : déterminez si la somme totale est un multiple de 10. D’après l’algorithme de Luhn, le numéro est considéré comme valide si le total se termine par 0.

Vérifions par exemple le numéro 79927398713 à l’aide de la formule de l’algorithme de Luhn.

En partant de la droite, et en commençant par l’avant-dernier, multipliez par deux un chiffre sur deux :

1 x 2 = 2

8 x 2 = 16 (1 + 6 = 7)

3 × 2 = 6

2 × 2 = 4

9 x 2 = 18 (1 + 8 = 9)

Additionnez tous les chiffres ensemble, y compris les chiffres non multipliés par deux :

7 + 9 + 9 + 4 + 7 + 6 + 9 + 7 + 7 + 2 + 3 = 70

Le numéro 79927398713 est valide, d’après l’algorithme de Luhn, car le résultat obtenu est 70, un multiple de 10.

Ces étapes constituent la « formule » ou procédure suivie par l’algorithme de Luhn pour valider ou générer des numéros.

Intérêt de l’algorithme de Luhn

L’algorithme de Luhn a révolutionné la validation des données et la prévention de la fraude dans de nombreux secteurs, notamment dans la finance, les paiements et les services publics.

Voici quelques raisons qui expliquent son intérêt :

• Précision des données accrue : l’algorithme de Luhn est une méthode de détection simple des types d’erreurs de saisie les plus courantes, telles que celles commises sur un chiffre ou les inversions de deux chiffres. Il est donc particulièrement utile dans certains secteurs comme la finance et la banque.

• Facilité de mise en œuvre : l’algorithme est simple à comprendre et à mettre en œuvre dans différents langages de programmation, sans mobiliser d’importantes ressources. Il est donc accessible pour un large éventail d’applications.

• Traitement des données en temps réel : l’algorithme de Luhn peut être appliqué en temps réel pour confirmer l’exactitude des données numériques au fur et à mesure de leur saisie. Ce type de vérification est devenu important pour les systèmes qui requièrent une validation instantanée des données.

• Prévention de la fraude : bien qu’il ne soit pas infaillible contre les tentatives de fraude sophistiquées, l’algorithme de Luhn agit comme une première ligne de défense. Il permet de détecter les numéros non valides avant qu’une transaction ou une opération ne soit effectuée, ce qui peut décourager les tentatives de fraude et réduire les erreurs susceptibles d’entraîner une fraude ou des failles de sécurité.

• Rentabilité : en détectant les erreurs en amont du processus, l’algorithme évite les coûts associés au traitement de données incorrectes (notamment des pertes financières), l’insatisfaction des clients et les coûts administratifs liés à la correction des erreurs.

• Adoption généralisée : en raison de son efficacité et de sa simplicité, l’algorithme de Luhn a été largement adopté dans le monde entier pour la validation des numéros d’identification par les principales sociétés de cartes de crédit, les agences gouvernementales et les institutions financières.

L’algorithme de Luhn est devenu un outil efficace pour vérifier les cartes bancaires et les données sensibles de par sa capacité à détecter les erreurs, à prévenir les fraudes et à garantir l’exactitude des transactions. Sa facilité de mise en œuvre et sa capacité de validation en temps réel en font une mesure de sécurité essentielle dans le traitement des paiements et les systèmes financiers.

Types de numéros validés par l’algorithme de Luhn

L’algorithme de Luhn est utilisable dans n’importe quel système qui requiert une saisie manuelle de numéros. Il fait office d’outil de validation en temps réel qui permet de détecter et de signaler immédiatement les erreurs, et ainsi d’améliorer la qualité des données et leur efficacité opérationnelle. Il permet de s’assurer que les séquences de numéros sont valides d’un point de vue structurel avant tout traitement ultérieur.

Voici un aperçu des différents types de séquences généralement vérifiés.

• Numéros de carte bancaire : l’utilisation la plus courante de l’algorithme de Luhn concerne la vérification des numéros de carte bancaire. Avant le traitement d’une transaction par carte bancaire, le numéro de carte est vérifié à l’aide de l’algorithme de Luhn afin de confirmer qu’il correspond à une séquence valide. Cette étape permet de détecter les erreurs de saisie accidentelles ou les numéros incomplets. Presque toutes les cartes bancaires intègrent une vérification basée sur l’algorithme de Luhn.

• Numéros d’identification : l’algorithme de Luhn est utilisé pour valider des numéros d’identification, tels que les numéros de sécurité sociale, d’IMEI, de téléphones portables ou d’identification nationale. Ce processus de validation vérifie que ces numéros ont été correctement saisis et traités.

• Identifiants financiers : de nombreuses banques utilisent l’algorithme de Luhn pour vérifier des numéros de compte et d’autres identifiants financiers tels que les numéros de routage avant de traiter des transactions telles que les transferts de fonds.

• Codes-barres : certains formats de codes-barres, tels que les codes EAN et UPC, comportent un chiffre de contrôle calculé à l’aide de l’algorithme de Luhn. Les scanners l’utilisent pour vérifier que les codes-barres sont scannés correctement. Ce type de contrôle est particulièrement pertinent pour le suivi précis des stocks, les passages en caisse dans un commerce de détail et certaines opérations logistiques.

Utilisation de l’algorithme de Luhn dans différents secteurs

L’algorithme de Luhn est utilisé dans de nombreux secteurs pour vérifier des données numériques d’importance critique, éviter les erreurs de saisie et renforcer la protection contre la fraude.

Voici un aperçu des applications pratiques de l’algorithme de Luhn :

• Achats en ligne : lorsque vous effectuez un achat en ligne, le système de paiement utilise l’algorithme de Luhn pour vérifier que le numéro de carte bancaire saisi est valide avant de traiter la transaction. Cela permet de réduire les refus de paiement dus à des erreurs de saisie ou à des numéros incorrects.

• Systèmes bancaires : les banques utilisent l’algorithme de Luhn pour valider les numéros de compte et de routage et s’assurer que les fonds sont transférés vers les comptes appropriés. Cette procédure permet de s’assurer que les fonds sont transférés sur des comptes financiers valides avant que les transferts électroniques de fonds (TEF) ou les paiements ACH ne soient traités.

• Téléphones portables : les numéros IMEI identifient les appareils mobiles et comportent un chiffre de contrôle calculé à partir des autres chiffres à l’aide de l’algorithme de Luhn. La vérification de l’intégrité du numéro IMEI permet de prévenir la fraude et d’identifier l’appareil lors de l’achat d’un téléphone d’occasion.

• Documents officiels : dans certains pays, des numéros d’identification, tels que les numéros de sécurité sociale ou les numéros d’identification nationale, comportent un chiffre de contrôle calculé à l’aide de l’algorithme de Luhn. Les administrations publiques peuvent ainsi vérifier l’exactitude de ces numéros lors de la saisie et du traitement des données.

• Entreprises de services publics : les fournisseurs de services publics utilisent souvent l’algorithme de Luhn pour valider les numéros de compte client. Ainsi, ils peuvent garantir que les informations de facturation et de paiement sont associées aux bons comptes, ce qui réduit les erreurs de facturation et les problèmes liés au service client.

• Systèmes de billetterie : les compagnies aériennes, ferroviaires et autres entreprises de transport utilisent l’algorithme de Luhn pour valider les numéros de référence des réservations ou des billets. Elles s’assurent ainsi que les données sont saisies correctement et limitent le risque de fraude.

Limites de l’algorithme de Luhn

Bien que l’algorithme de Luhn soit un outil puissant de détection des erreurs et de validation numérique, il présente certaines limites. En matière de détection de la fraude ou de validation des données, l’algorithme de Luhn ne constitue généralement qu’un élément parmi un ensemble plus vaste de contrôles et de mécanismes de vérification. Il ne doit pas être utilisé comme unique moyen de protection pour les applications dont la sécurité est un enjeu majeur.

Les principales limites de l’algorithme de Luhn en matière de validation des données sont précisées ci-dessous.

• Détection des erreurs complexes : l’algorithme est conçu pour repérer les erreurs courantes, telles qu’une erreur de saisie d’un seul chiffre ou l’inversion de deux chiffres adjacents (par ex., 67 devenant 76). Cependant, il ne détecte pas les erreurs plus complexes, telles que la permutation de chiffres non adjacents (par ex., 197 devenant 971) ou la présence de plusieurs chiffres incorrects dans une séquence.

• Détection de la fraude : l’algorithme de Luhn peut vérifier qu’une séquence de chiffres est potentiellement valide, mais il ne peut pas déterminer si elle correspond à un compte ou à une identité légitime, ni protéger contre les activités frauduleuses intentionnelles lorsqu’un fraudeur dispose d’une séquence de chiffres valide.

• Données non numériques : l’algorithme s’applique uniquement aux données numériques et ne peut pas être utilisé pour valider des données qui incluent des lettres, des symboles, des caractères spéciaux ou des identifiants alphanumériques.

• Intégrité des données : l’algorithme vérifie uniquement la validité numérique et non l’intégrité des données. Il ne peut pas détecter de modification intentionnelle éventuelle ni identifier la partie incorrecte de la donnée.

• Prédictibilité : l’algorithme est une méthode standard bien connue et toute personne qui en maîtrise le principe est en mesure de générer des numéros qui seront validés par la formule de Luhn. Cette prédictibilité peut constituer un désavantage dans certaines situations où un niveau de sécurité supérieur est requis.

• Application limitée pour la cybersécurité : étant donné que la vérification par la formule de Luhn ne chiffre ni ne dissimule les données, elle n’offre pas de sécurité contre les attaques telles que le piratage, l’hameçonnage ou les violations de données. D’autres mesures de sécurité, telles que le chiffrement, l’authentification multifacteur (MFA) et la détection de la fraude par l’IA, doivent être utilisées en parallèle.

Malgré ces limites, l’algorithme de Luhn reste un outil largement utilisé pour les vérifications préliminaires des séquences numériques dans diverses applications, en particulier dans les services financiers. Associé à des processus de sécurité et de vérification supplémentaires, il peut contribuer à améliorer l’exactitude des données et à prévenir les erreurs accidentelles dans les séquences numériques.

Comment Stripe Radar peut vous aider

Stripe Radar utilise des modèles d’IA entraînés à détecter et à prévenir la fraude, en utilisant les données du réseau mondial de Stripe. Ces modèles sont continuellement mis à jour en fonction des dernières tendances de fraude, protégeant ainsi votre entreprise à mesure que les techniques évoluent.

Stripe propose également Radar Plus, qui permet aux utilisateurs d’ajouter des règles personnalisées pour traiter des scénarios de fraude spécifiques à leur entreprise et d’accéder à des analyses avancées sur la fraude.

Radar peut aider votre entreprise à :

• Prévenir les pertes dues à la fraude : Stripe traite plus de 1 000 milliards de dollars de paiements par an. Cette échelle permet à Radar de détecter et de prévenir efficacement la fraude, vous permettant ainsi de réaliser des économies.
  
• Augmenter les revenus : les modèles d’IA de Radar sont entraînés sur des données réelles de litiges, des informations clients, des données de navigation, et plus encore. Cela permet à Radar d’identifier les transactions risquées et de réduire les faux positifs, augmentant vos revenus.
  
• Gagner du temps : Radar est intégré à Stripe et ne nécessite aucune ligne de code pour être configuré. Vous pouvez également surveiller vos performances antifraude, écrire des règles, et plus encore dans une plateforme unique, augmentant l’efficacité.
  

En savoir plus sur Stripe Radar, ou démarrez dès aujourd’hui.